How do You Improve Math Text Accessibility?
Imagine the experience of a beginning reader, a child with dyslexia, or a multilingual learner encountering the following grade 1 word problem while working independently.
| Read the math story and make a simple math drawing with labels. Circle 10, and solve the problem with a number sentence. |
| Marianne goes grocery shopping. She buys 5 apples and 2 bananas. Then she buys 8 oranges. How many pieces of fruit does Marianne have altogether? |
Consider the student’s perspective. What factors impede the student’s access to the mathematical content? How does this experience of struggling to read the problem contribute to the student’s identity as a young mathematician?
For a student, the sentence complexity might present a challenge. Students may not be able to decode words such as circle, Marianne, grocery, shopping, fruit, or altogether. Phrases like goes grocery shopping or solve the problem with a number sentence may bewilder a multilanguage learner: “Goes where?” “How do I solve a problem with a sentence?” While the math content in this word problem is appropriate for a grade 1 math curriculum, the reading level does not match grade 1 reading expectations; the language is more appropriate for students in grades 3, 4, or even 5.
Students may not see what the point of the problem is—adding three parts—if they are working hard to decode and comprehend the text. In other words, the mathematics can get lost as students work through the words. A student may already understand how to add three quantities to find a total, as they are asked to do in this word problem. They may even have a good grasp of strategy, such as adding 8 and 2 first to make ten. However, a student may spend so much time and cognitive load parsing the context that they are tired or rushed by the time they reach the math portion of the word problem, growing frustrated and disengaged. Their identity as a mathematician is undermined rather than affirmed, and their math knowledge is unable to shine through.
Now, consider this word problem from your perspective as an educator. How does the inaccessibility of this word problem affect your quality of instruction? What could be possible in your classroom if the text were accessible to all students?
Rather than observing student work and engaging with learners, you may find yourself spending instructional time helping students read the directions and the text of the problems. You may find yourself rewriting word problems for students during precious planning time. If the text in the word problem were accessible, your instruction time might look very different. You could spend your planning time studying the mathematics, developing ideas for engagement, customizing lessons based on data, and differentiating instruction in small groups. Students would feel empowered as mathematicians to independently solve problems and engage with their peers.
At Great Minds®, we believe that all students should see themselves as mathematicians and be able to engage with math text such as problem directions and word problems. Eureka Math²™ was developed with readability and accessibility as a priority to ensure that all learners can focus on building math knowledge and understanding. By using readability best practices and accessibility tools to reduce and eliminate extraneous words and by increasing visual supports, the curriculum writers have ensured the cognitive load is centered on the mathematics, empowering students to embrace the challenge of every problem.
Both students and educators face barriers because of readability issues. A well-designed high-quality curriculum can remove many of those barriers. Eureka Math² is designed to be a well-designed high-quality curriculum.
What is Readability in Math?
Too often, math materials do not address the learning needs of all students, including emerging readers and students reading below grade level who may benefit from text designed to be accessible. Joan M. Kenney, Euthecia Hancewicz, Loretta Heuer, Diana Metsisto, and Cynthia L. Tuttle point out in their book, Literacy Strategies for Improving Mathematics Instruction, “Research has shown that mathematics texts contain more concepts per sentence and paragraph than any other type of text. They are written in a very compact style; each sentence contains a lot of information, with little redundancy ... . Finally, many texts are written above the grade level for which they are intended (Barton & Heidema, 2002).”
Eureka Math² is different. The teacher–writers behind Eureka Math² believe a student’s identity as a mathematician should not be dictated by the readability of a curriculum. Great Minds, in partnership with educators, is committed to creating a culture of access and equity in classrooms by improving the readability and accessibility of text while maintaining grade-level rigor. This critical, often overlooked work of readability ensures that every child can engage in all components of instruction, see themselves as a mathematician, and delight in doing math.
The teacher–writers of Eureka Math² have developed the most readable mathematics curriculum on the market. Students who are learning to read (grades 1 and 2), students who are reading below grade level, readers with dyslexia, multilingual learners, students with processing challenges, and students overwhelmed by dense print, among others, all benefit from the increased accessibility and readability of the text. Our goal is to lighten the cognitive load of reading so students can focus on the math.
Student-Friendly Pages
To enhance readability while maintaining rigor and focus on grade-level content, the Eureka Math2 writers included ample white space on student pages, paid careful attention to phonics patterns and sight words, added visual supports when necessary, and used concise sentences.
Consider the following word problem taken from Eureka Math² grade 1. Note that the nonmathematical context is simplified, the words are easier to read, the sentences are short, and there is one sentence per line. The concise directions of Read–Draw–Write are repeated in the same format in every word problem. The visuals—in this case the pictures of fruit—support students who are not yet confident readers, but the words are still present for students who are. This word problem exemplifies how the curriculum was constructed to meet the accessibility and readability needs of all learners.
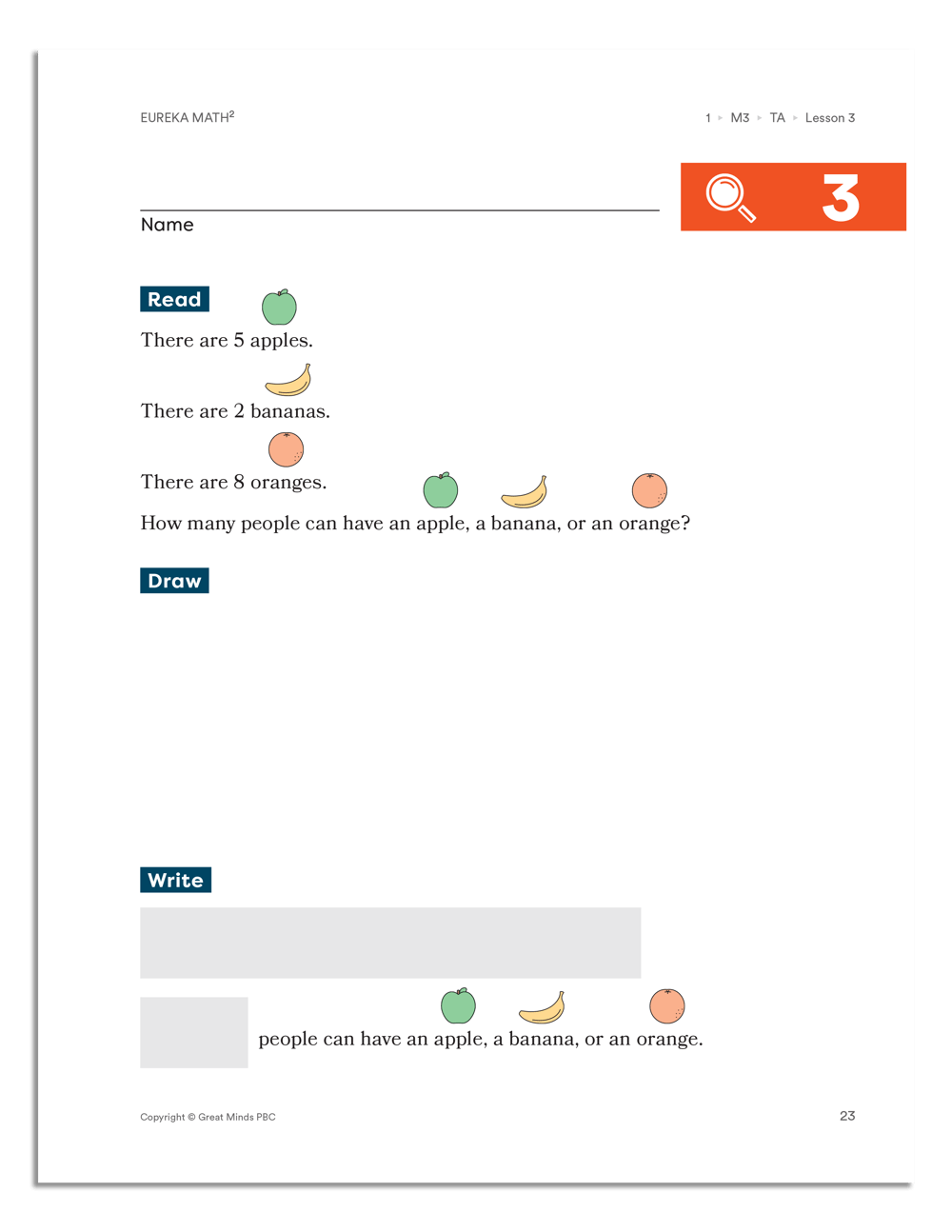
What is in a Readability and Accessibility Toolbox?
When building Eureka Math² with an explicit focus on readability and accessibility, the curriculum writers prioritized four key elements:
- Syntax and structure
- Semantics
- Decodability
- Layout
Syntax and Structure
Syntax and structure refer to the arrangement of words that come together to express a complete thought or sentence. Simple sentence structure (where the subject comes first, followed by the verb, and then the object) is easiest for readers to follow.
Eureka Math² uses simple sentence structure whenever possible. In the lower grades, each sentence appears on its own line to give space for students to process and make sense of what they read. Words that do not contribute to the mathematical meaning of the sentence or the rigor of the problem were eliminated. The examples below highlight the improved syntax and structure used in the early grades.
| Before | After |
| Sierra has 1 rock in her collection. She finds 4 more rocks to add to her collection. Via has 9 rocks in her collection. how many rocks do the friends have altogether? |  |
| Before | After |
| To earn money, Travis does chores. He earns $6 a week for 4 weeks, and he earns $4 the fifth week. How much money does he earn doing chores? | Travis earns money doing chores. He earns $6 each week for 4 weeks. He earns $4 the fifth week. How much does Travis earn altogether? |
Notice how the revised problems don’t sacrifice mathematical rigor? Readable problems can be just as challenging as complicated, unreadable ones.
Semantics
Semantics refers to the meaning of a word, phrase, or sentence. Words can have multiple meanings. For this reason, contexts avoid less familiar multiple-meaning words (e.g., consume, yield, log, revolutions) and similar-sounding words (e.g., sale, sail;). In addition, content-critical terminology is introduced in context to help students build understanding. Familiar terminology is intentionally used repeatedly and encouraged in sentence frames and similar supports so students become accustomed to using precise mathematical language.
To keep the nonmath cognitive load low for students, Eureka Math² limits the introduction of new noncontent-related terminology. When language support for a new nonmath content term was needed, the writers included an image or video to accompany the problem. Many margin notes offer instructional support suggestions in the Teacher Edition.
The example below highlights how the Teacher Edition supports multiple-meaning words. The curriculum identifies multiple-meaning words explicitly for teachers and then goes a step further to show how to help students access the word and its meaning in the context of the math problem.
The following example shows how visuals are used to support students in comprehending nonmath terminology in word problems. In this example, a picture of a watermelon and a pineapple support the reading and meaning making of the word problem.
Repeated use of familiar contexts and terminology was intentional. For example, the contexts of being at the park, at home, at school, at a theater, and on an airplane are used repeatedly in a grade so students do not have to learn a new context and its associated terminology. In addition, word problems repeatedly feature the same activities, such as playing with friends, planting a garden, following a recipe, and shopping, so students spend less time making sense of context and more time on the math, as in doing fraction work associated with recipes and determining a discount.
Decodability
Early readers are more successful with text that they can decode—that is, text that contains familiar phonetic (sound-spelling) patterns and sight words. While decodable text is critical in English language arts (ELA) instruction as students are exposed to and become fluent with new phonetic patterns, it is also a critical consideration in math curricula. Eureka Math² uses a controlled vocabulary that includes only phonetic patterns and high-frequency sight words familiar to students from their ELA sequence.
In grades 1 and 2, the curriculum team examined major reading foundational skills programs and synthesized a detailed two-year quarterly phonics progression to guide the writing of student pages. Generally speaking, there are no decodability guidelines for grades 3–12. However, the curriculum still limits multisyllabic words (instead of marker, use pen; instead of collects, use gets), irregular spelling patterns, and difficult phonemes.
The careful attention to decodability throughout the curriculum is evident in the student names used in word problems, shown in the chart below. In addition to using decodable names, the same names are repeated throughout the curriculum so that students don’t have to learn to read new names with every word problem. Further, the names used in word problems and as example students in the lesson vignettes are intentionally diverse to represent all students who learn with the curriculum.
|
K–2 Names |
3–5 Names |
6–9 Names |
|
Bev Zan Mac Kat Jade Hope Sal Lee Tam Baz Lan Ming Ren |
Deepa Jayla Mia Oka Zara Pablo Sasha Jada Riley Noah Yuna Lacy Gabe |
Shawn Noor Abdul Pedro Kabir Zara Hana Ji-Won Haru Kota Laya Theo Tiah |
| Note: This chart is not exhaustive of all names used in the curriculum. | ||
By using decodable text, a curriculum ensures that students can move beyond the context and into the work of learning math and gives educators more time to support students in building math knowledge. 
Layout
One reason the student pages of Eureka Math² are welcoming to students is the way the pages are designed. Multiple layout components were designed to optimize the student experience, including chunked blocks of text; images; increased white space; bullets, tables, and headings; and easily readable fonts and font sizes. Eureka Math² was designed to meet the needs of students as they grow. One teacher who piloted Eureka Math² saw the impact of the page layout on her students: “The main difference I see is that the student pages are more student friendly with more visuals and less print on each page. This is more accessible to the students and allows them to complete [the student pages] more independently without being overwhelmed."
When students can access the text, they are empowered to access rich and complex content. EdReports.org, a curricula-rating company, states one of their curriculum review criteria for quality as “the visual design (whether in print or digital) is not distracting or chaotic, but supports students in engaging thoughtfully with the subject.” Eureka Math² increases readability by thoughtfully arranging text, white space, writing supports, and visual supports.
Print edition materials of Eureka Math² use a readable font. The size of the text is developmentally appropriate—large and easy to track for emerging readers and then reduced slowly until grade 3, where the size and text structure anticipates a more confident reader. In addition to using readable fonts, the student pages include a limited amount of text. In grades K–2, sentences are written on their own lines. Starting in grade 3, students can be expected to track sentences to the next line. Student-facing directions are kept simple, but they sometimes include necessary math content words or other words outside the readability guidelines. Therefore, teachers may read directions aloud to students as appropriate.
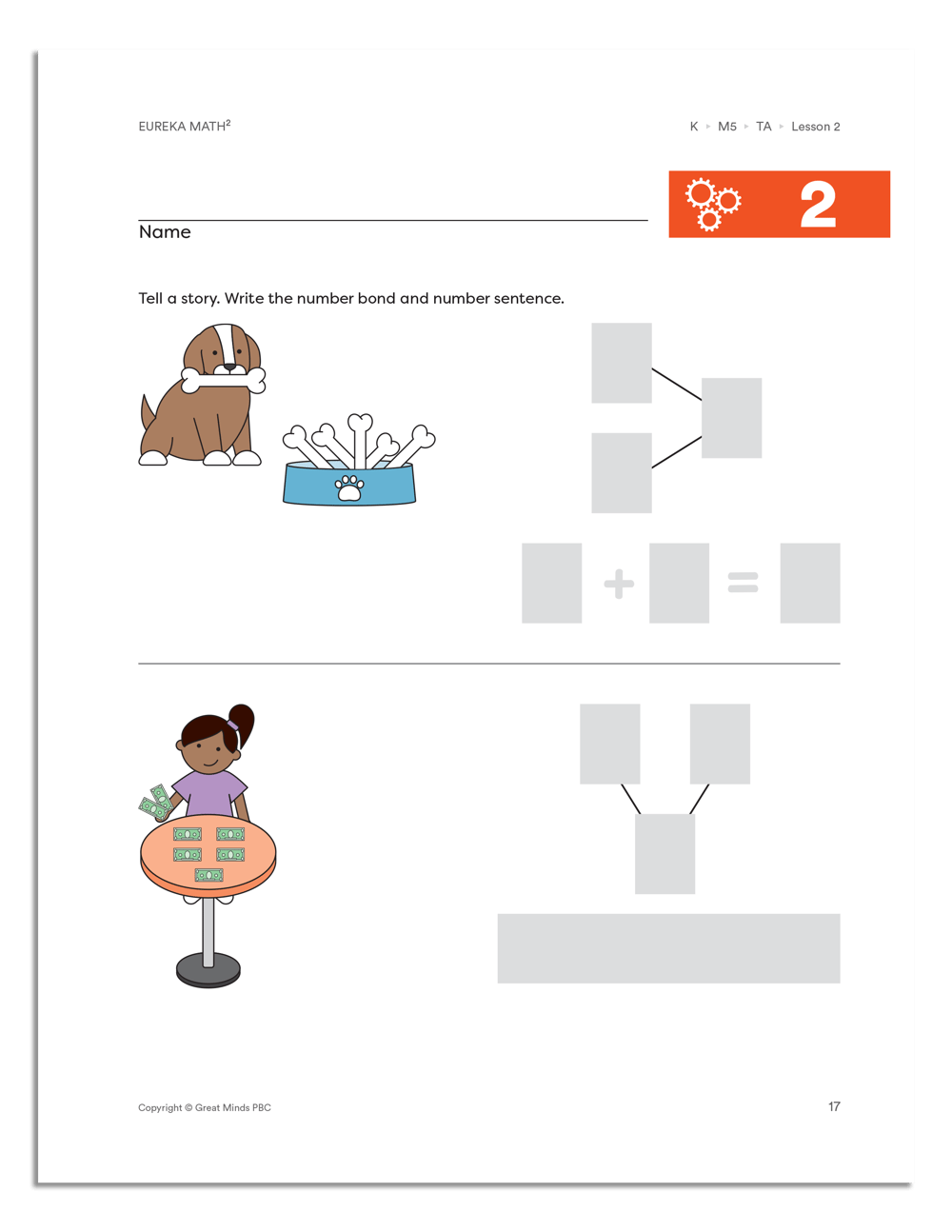
Students in kindergarten and grade 1 are provided with writing support through gray boxes (as seen in the example to the left). The pages also include plenty of white space for students to work and show their thinking through numbers, pictures, or words.
While readable fonts and limited text support students in reading the words on the page, visual supports are included when needed in grades 1 and 2. In the example, visual supports have been implemented for cats, dogs, and fish so that students can access the text and focus on the math.
The commitment in Eureka Math² to a student-friendly layout and experience allows students to focus on their math learning and sharing their thinking. A grade 1 teacher piloting the curriculum said that “[fewer] examples on a page, more visuals, and more white space allow students to access the activity and focus on the math concepts rather than reading and wordy directions. More space is there for students to authentically share their thinking through drawings, number sentences, etc.” Even the best math program can introduce barriers with a cramped or confusing layout, but the new, sleek layout of Eureka Math² ensures that students can excel on every page.
How do You Ensure Readability Doesn't Compromise Rigor?
A math curriculum should be designed to teach mathematics, not reading. However, students must often read directions and word problems in mathematics. Educators often raise the concern that such text is not accessible to students. Eureka Math² strives to support teachers and students by increasing the readability of student text without compromising intellectual rigor. In other words, the words and layout are not a barrier to high-quality mathematics. Each student page is intentionally crafted to be accessible and contain rich, relevant, and rigorous mathematical content. Rigor and readability go hand in hand, helping students build knowledge and achieve greatness.
Download the Article as a Free PDF
Great Minds
Great Minds PBC is a public benefit corporation and a subsidiary of Great Minds, a nonprofit organization. A group of education leaders founded Great Minds® in 2007 to advocate for a more content-rich, comprehensive education for all children. In pursuit of that mission, Great Minds brings together teachers and scholars to create exemplary instructional materials that provide joyful rigor to learning, spark and reward curiosity, and impart knowledge with equal parts delight.
Topics: math
Get the Latest Great Minds Updates
Stay informed of simple yet crucial implementation support tips, curriculum updates, new resources, professional development opportunities, and more for math, science, and ELA.
