As teachers, we ask a lot of questions. It’s part of the job. It’s how we learn about our students.
Questions serve a variety of purposes during instruction. We can use questions at the beginning of an activity to launch a task, during a lesson to informally assess, and while providing feedback to advance student thinking. Let’s look at how we can use intentional and purposeful questions to set students up for success, assess their understanding, and push their learning forward.
Questions help set up a math task and engage all students in the task.
At the beginning of a lesson or task, we ask questions to orient students and ensure they understand what they need to do. These questions also build engagement and buy-in from students. You might launch learning by asking questions like the following:
- What do you notice about the problem?
- What do we mean by _____?
- What are we trying to figure out?
- How is this task similar to one we’ve completed before? What’s new or different?
These questions open entry points into the activity for all students. They stimulate student thinking without lowering expectations by prompting or suggesting a specific solution path.
Questions allow teachers to individualize assessment and instruction.
As students work on math problems, you likely circulate throughout the room and monitor their progress. This is a great opportunity to ask questions to formatively assess and extend student thinking.
|
Assessing questions provide information about students’ knowledge and skills and help clarify what students understand about the work. |
Advancing questions push a student to think in new ways to build their knowledge. |
|
The following are general examples of assessing questions:
|
The following are general examples of advancing questions:
|
| Assessing questions can also help you find patterns in student work and inform how you conduct the Student Debrief or Lesson Closing. |
Advancing questions naturally create differentiation because they allow you to meet students at their current point of success and move their thinking forward. |
Let’s look at a specific example to clarify the roles of assessing and advancing questions. As you review the following work of three different students on a Grade 5 fraction problem, think about what each student might know and what would further extend their learning.
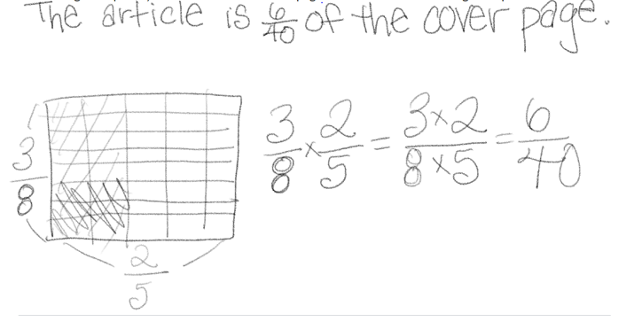
A newspaper’s cover page is 3⁄8 text, and photographs fill the rest. If 2⁄5 of the text is an article about endangered species, what fraction of the cover page is the article about endangered species?
Student A
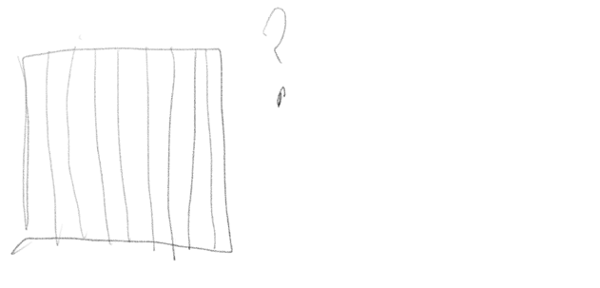
Student B
Student C
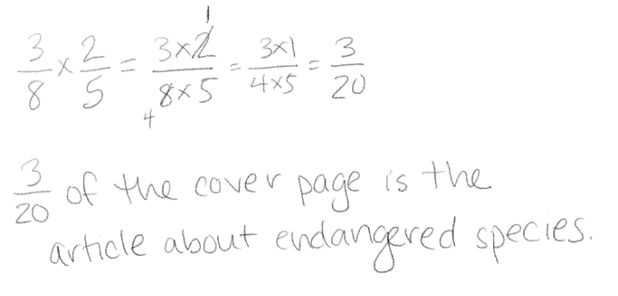
Students A and C arrived at a correct answer, but Student C identified a common factor in both the numerator and denominator, which resulted in a more simplified answer. Student A seems to have labeled the drawing incorrectly but still performed the correct multiplication. Student B is struggling to get started. Here are some questions you can ask to assess or advance each student.
|
Assessing Questions |
Advancing Questions |
Student A
|
|
Student B
|
|
Student C
|
|
Although each student’s response was unique, we found ways to advance each student’s thinking through questioning. Posing questions promotes reflection and thinking that will lead to deeper conceptual understanding and more meaningful connections between mathematical ideas. While every student is different, every student is capable of greatness. With well-placed, purposeful questions, we can advance each student’s learning and help them achieve their greatness.
Amy Bustard
Amy Bustard is a Eureka Math Implementation Leader. She specializes in supporting remediation and the development of cognitive and executive functions skills for students in all grade levels.
Topics: Implementation Support
Get the Latest Great Minds Updates
Stay informed of simple yet crucial implementation support tips, curriculum updates, new resources, professional development opportunities, and more for math, science, and ELA.
