Grading in Eureka Math®

As teachers, we know that grading is a required part of our work. When I first started teaching, the biggest mistake I made was to grade everything my students completed. I quickly learned that my approach was unsustainable and ineffective. I had to change my grading practices and even my beliefs about grading. I learned to make sure that my grading is equitable, meaningful, and accurate, and I learned to be selective about what I graded. I’ll share with you what I discovered about providing opportunities for practice, giving appropriate feedback, and carefully choosing what to grade and how to grade it when using Eureka Math^®.

Practice and feedback come before grading.

Give students ample opportunity to practice and to incorporate feedback you’ve given before assigning a graded task. This method promotes equity because some students arrive at proficiency more slowly than others. A graded task should reflect the end product of learning instead of the steps along the way. With nongraded practice and feedback, students enjoy a safe learning environment in which they are not penalized for missteps on their road to proficiency. Ultimately, the grade reflects only the culmination of their learning, measuring the ultimate proficiency that has developed over time, not the mistakes some of them needed to make to achieve it.

Make practice and feedback routine.

You may think of practice as the homework students do outside of class. But practice happens throughout lessons in Eureka Math’s Concept Developments, Sprints, Problem Sets, Application Problems, Student Debriefs, and Exit Tickets. Make a habit of simply providing feedback to students on their practice work instead of assigning points or a letter grade. Your feedback can be verbal or written. Often, it will be quick. It should be targeted to help students reconsider mistakes or challenge them to go deeper, go further, or be more efficient when they demonstrate understanding.

For instance, consider the practice problem and student work shown, which was taken from a Grade 4 Exit Ticket.

In January, Scott earned $8,999 . In February, he earned $2,397 more than in January. In March, Scott earned the same amount as in February. How much did Scott earn altogether during those three months? Is your answer reasonable? .

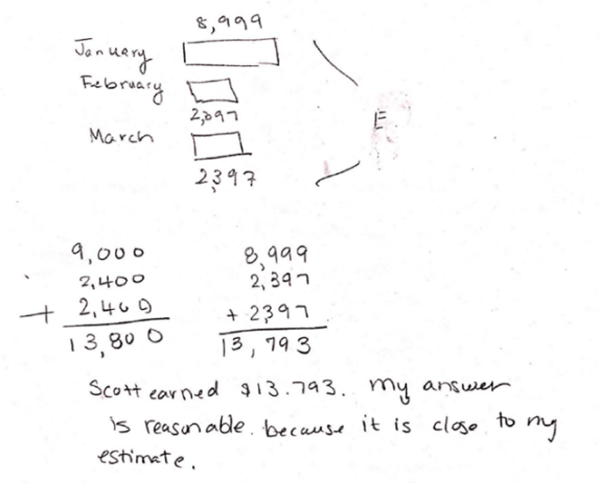
While your knowledge of the student should inform your feedback, some appropriate guidance for the student might include the following:

• Read the problem again. Does Scott make more money in January or in February?
• Your addition is correct, but I’m not sure you used the correct numbers. How did you decide what numbers to add?
• In the second sentence of the problem, what does the word more indicate for this situation? Think about that and decide whether you might need to change some of your work.

Ungraded practice and feedback give students meaningful guidance to adjust their thinking about math. Providing feedback instead of grading also helps you adjust your teaching to better support individual students and keep everyone on track.

Be selective about what you grade.

Choose to grade content only after students have had adequate practice and feedback. Often, that means giving a graded topic quiz or module assessment. If you need to create an assessment, a simple option is to repurpose unused problems from previous lessons. For example, the problems could come from Problem Sets or Homework. You might also look at Application Problems or Exit Tickets you’ve used and write similar problems with different contexts or numbers. Choosing problems in this way supports meaningful grading because students have already been given time to practice and consolidate their thinking before being evaluated. Additionally, the problems you’re grading align with the Eureka Math lessons and learning outcomes.

Be fair and accurate in your grading.

To promote fairness when you grade student work, think beyond just correct or incorrect answers. To promote accuracy and mitigate subjectivity with grades, identify in advance the criteria you’ll use to determine where the students are on their path to proficiency. Did they use a strategy that could have led to a correct answer but didn’t? Are they able to support their answer with explanations or drawings? Is an answer incorrect because of a computation error or a conceptual misunderstanding? Take these many criteria into account, and get comfortable with giving partial credit.

Another way to ensure equity is to allow students to retake graded assessments after additional learning has taken place. Your students may obtain proficiency at different times. Since students’ understanding deepens over time, retakes provide the most accurate and up-to-date data. This practice focuses grades on actual academic outcomes rather than giving just a snapshot in time. It sends a message to students that they can and should continue to learn even after an assessment is graded.

The most rewarding aspect about shifting my grading practices was the change in my students’ motivation and the overall culture of my classes. Students were less anxious and less stressed about their grades because they knew that my grading practices were equitable, meaningful, and accurate. Students also recognized that the focus of my classes was on the overall learning process.