As a Grade 5 teacher, I had the same frustration year after year: My students were not fluent in their basic math facts. They performed many operations by using their fingers—a process that can be slow and cumbersome. Watching them struggle made me think about what fluency is and how I could help my students become fluent with math.
Fluency is more than memorization.
The position statement of the National Council of Teachers of Mathematics on Procedural Fluency in Mathematics calls out fluency as a critical component of mathematical proficiency. Fluency can be thought of as the ability to compute and apply procedures accurately, efficiently, and flexibly in different problems and in different contexts. So fluency is more than just memorization, speed, and accuracy.
Fluency requires that students understand the properties of mathematics and can use those properties to find solutions in various ways. Consider two examples of student thinking to solve .
“I know that the first addend needs more to make . I can get the from the other addend , which leaves . So and is , and more is .”
“I can use what I know about doubles facts to help me solve this problem. I can take from the and give it to the . That makes plus , which I know equals .”
These students may not have memorized all the addition facts, but their responses show evidence of fluency with addition. The students are accurate, reasonably quick, and flexible in their reasoning about the problem.
It takes intentional planning and repetition to help students develop mathematical fluency. Eureka Math® uses a variety of fluency routines as part of daily instruction. Let’s consider a couple of tips that can help you get the most out of fluency routines.
Be responsive to students during fluency activities.
Sometimes we plan for a fluency activity and then just go with our plan without making adjustments based on what students do during the activity. The best fluency activities happen when you’re responsive to your students. Let’s use Happy Counting as an example.
Happy Counting Instructions (for counting by ones)
Let’s play Happy Counting! We’re going to count by ones. When I hold my hand like this (point thumb and motion up), I want you to count up. If I put my hand like this (point thumb and motion down), I want you to count down. If I do this (thumb to the side), that means stop, but try hard to remember the last number you said.
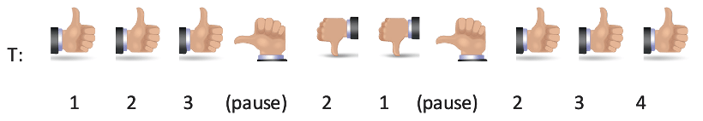
At first, I didn’t really understand how I could be responsive to the needs of my students during this routine. My class worked through predetermined number sequences, and I might have even counted along with my students. Later, I learned to just give hand signals, watch, and listen to my students. Then I adjusted my sequences based on what I observed. Here are some ways I was responsive.
|
My Observation |
My Response |
|
The class was not in sync during the count. |
I slowed the pace of the count and ensured that hand signals were clear. |
|
Students made errors with key transitions such as crossing over the ten. |
I repeated the transition several times before moving on, for example, using the short sequence 28, 29, 30, 31, 32, 33 to provide practice with crossing over the ten three times. |
|
A few students made errors when they counted by a certain value, such as . |
I wrote multiples of the value (e.g., 7, 14, 21, 28,…) on sticky notes and placed the notes on those students’ desks. |
|
Students were slow to state the next value. |
I provided think time, pausing and asking the class to raise their hands when they knew what came next. |
These adjustments to my delivery supported my students and helped them succeed with Happy Counting. Regardless of the fluency routine you use, observe your students and be responsive to them in the moment.
Choose problems for a white board exchange with intention.
I probably use the White Board Exchange (WBE) more than any other fluency routine. I love that the WBE holds every student accountable for a response. It took me some time to learn that a WBE is more than just students using individual white boards to do their work. As teachers, we must intentionally craft sequences of problems for WBEs so that each problem is a bridge to the next. Look at the sequences of the following problems for examples of WBEs at different grade levels.
It takes time and practice to create these intentional sequences. A helpful tip is to use an aspect of previous problems to set students up for success on the next one. You can increase the challenge throughout the sequence and at the same time help students recognize the relationships between the problems.
Developing fluency takes time, so don’t expect students to become fluent after one activity. Eureka Math uses a variety of strategies to ensure that students build fluency. The more you work with these fluency routines, the more intentional and responsive you’ll become with them.
Jessica Jeffers
Jessica Jeffers is a Eureka Math implementation leader. She's a former Grade 5 teacher and math coach.
Topics: Implementation Support
Get the Latest Great Minds Updates
Stay informed of simple yet crucial implementation support tips, curriculum updates, new resources, professional development opportunities, and more for math, science, and ELA.
