Reducing Unproductive Struggle and Maintaining Rigor

Words can’t even begin to describe the frustration I felt as both a special education teacher and an instructional coach when I saw students struggle in and fear math class. Over time, I realized that the anxiety students faced every day had little to do with their ability to do the math. That anxiety was more about students’ ability to access the math. I realized that I needed to help my students overcome their constant battle to access the content. I needed to stop perpetuating their feeling that they would never get it right. I needed to change their mindset that math isn’t even worth trying.

So let’s get to the root of this problem and address some simple ways to approach it.

Unproductive struggle gets in the way of learning math.

Unproductive struggle occurs when reading, writing, anxiety, or other skills unrelated to math get in the way of students accessing mathematical content. For example, think about students who read below grade level. If they can’t read a word problem, then they can’t plan how to solve it. Or perhaps students can read the problem but struggle with writing. When those students are asked to write about their solution to a math problem, they will likely offer a watered-down, simplified response. That kind of response doesn’t reveal the full scope of the student’s thoughts about the problem or their ability to do the math.

Adapt math problems to account for reading problems.

Let’s consider some ways to remove the unproductive struggle that gets in the way of your students accessing the math content. These simple adjustments will allow them to explore and learn the math.

Read the following Grade 4 problem in both its original and modified forms. What changes do you notice? What stayed the same?

Modify reading levels.
First, we adjusted the original problem to limit the potential for unproductive struggle with reading the problem. To do that, we changed the context and simplified vocabulary. The restaurant and omelets became an ice cream truck and ice cream cones. But the numbers and mathematical thinking stayed the same.

Chunk information and use white space.
In addition, we changed the layout of the problem. We chunked each piece of information by placing white space between each sentence. That makes the text easier to read—it’s less overwhelming, and students are more likely to believe they can decode the information. Again, the math stayed the same.

Make choices that maintain mathematical rigor.
We did not change the numbers, math vocabulary, or calculations at all. As we adjusted the reading difficulty of this problem, we considered what language was math terminology and what was simply context. We decided that restaurants and omelets related only to the context and could be changed. But we determined that the words more, fewer, and thousand, as well as the question words How many, were intentional math terminology that needed to stay.

Adapt problems to focus on the mathematical purpose.

Sometimes numbers that don’t affect the mathematical purpose of a problem get in the way. Just as we focus on important math terminology and subordinate nonmathematical contexts, we focus on the larger math concepts and subordinate individual calculations. This decision is based on the purpose or objective of the lesson. Let’s revisit the same word problem and consider what an adaptation based on math concepts might look like.

If the lesson objective is for students to solve comparison word problems, then we can adjust the problem to help students focus on comparison and the relationships between parts and wholes. As you read the original problem and the adapted problem that now focuses on comparison, notice what changed and what did not.

Changing the numbers in the problem keeps the focus on comparison but makes the calculations simpler. Students have access to the mathematical concept, and the problem now serves as a stepping-stone to build confidence and help students get to the complexity of the original problem. Making the calculations less complicated can also reduce math anxiety so students are more likely to try to solve the problem.

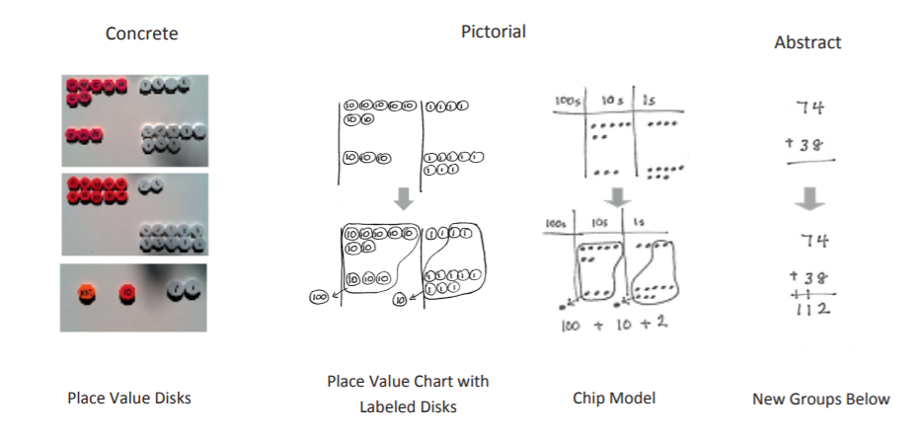
Adapt problems by using the concrete–pictorial–abstract approach.

What if the math objective includes arithmetic? In that case, you want students to reason through and use an algorithm to solve the problem. If arithmetic is the focus, and some students struggle with calculations, we can adapt the problem by using a different approach. We can make the algorithm more accessible by using the concrete to pictorial to abstract progression.

The original word problem requires students to regroup across place values as they calculate. Some students may need more concrete tools, such as stick bundles or place value disks, to understand this concept. Other students may need to take a pictorial approach by using a place value chart with labeled disks or by using a chip model. Both approaches meaningfully represent what happens as students add or subtract multi-digit numbers. Understanding the process conceptually helps students make fewer errors and identify the errors they do make. Eventually, we want students to solve math problems by using a more abstract approach. So if we properly scaffold the task for students, they can progress from an accessible starting point to mastering the grade-level content the objective requires.

Designing accessible math instruction is not about boiling a task down to a simplistic sequence of steps. Nor is it about making the task easier for students who struggle. Designing accessible math instruction requires that we remove barriers to accessing the math without undermining the objective. Once students are able to access the math, they are on the path to working on the grade-level content.