Supporting Students with Mathematical Models

The Eureka Math^® curriculum uses an intentionally selected set of versatile models to support students’ learning and problem solving. These mathematical models support students’ learning and problem solving. They help students think about mathematical relationships, understand concepts, and make connections. Models can promote student engagement with many of the Standards for Mathematical Practice. For example, they help students make sense of problems, reason quantitatively, use appropriate tools strategically, and make use of structure.

Eureka Math highlights a limited set of adaptable models because of the mathematical power they bring and for their accessibility for students. These cornerstone models include the number bond, number line, area model, and tape diagram. Of course, these models aren’t the only ones students can use, but they are intentionally emphasized for their versatility and flexibility. Students can use these models throughout their academic career.

Let’s explore some ways you can use models to help your students make sense of mathematics.

Use related models to support students.

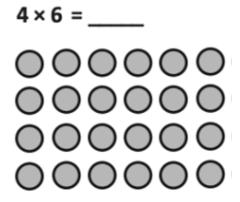
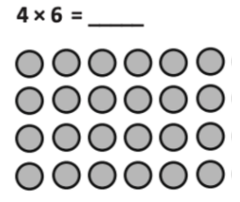
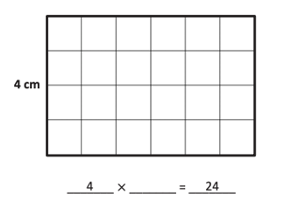
Many models in Eureka Math models evolve over time to match students’ growing mathematical understanding For instance, students’ work with arrays, to represent repeated addition in grade 2, scaffolds up to using the area model to represent the distributive property and multiplication and division with whole numbers, fractions, and decimals in later elementary. The area model is a scaffold to the tabular model students can use to multiply polynomials. These three models are all closely related. Each time students engage with a new model in this sequence, they build on prior knowledge and lay a foundation for future learning. The sequence of these three models can be leveraged to provide support for all students. For example, a student who needs support in using the area model can work with an array model as a scaffold. Similarly, high school students may benefit from reviewing the familiar area model before they begin using the tabular model for polynomials. Understanding how models relate to one another gives teachers the power to use related models to fully support students.

        

Use differentiated models to meet students’ needs.

Think about models as representations that support student thinking along a continuum from concrete to more abstract. When students require support with a concept, think about adjusting the representation to match their needs. For example, consider students working on part-whole relationships. If students have difficulty drawing or interpreting these relationships with a tape diagram, consider adjusting the representation to show the relationships differently. Draw the values using dots rather than labeling with a number, or use linking cubes to show the quantities more concretely. As students build depth of understanding and work on more complex mathematics, their representations can become increasingly abstract.

Using a consistent set of models that evolves with students intentionally creates scaffolds. When concepts feel new or more complex, the models are familiar tools that students can use to make sense of the mathematics

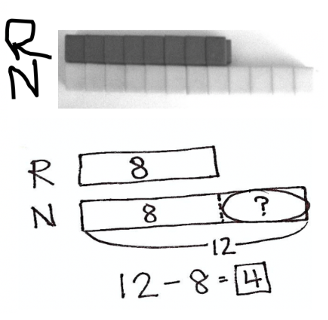
Support students by clearly making the connection between representations and models.

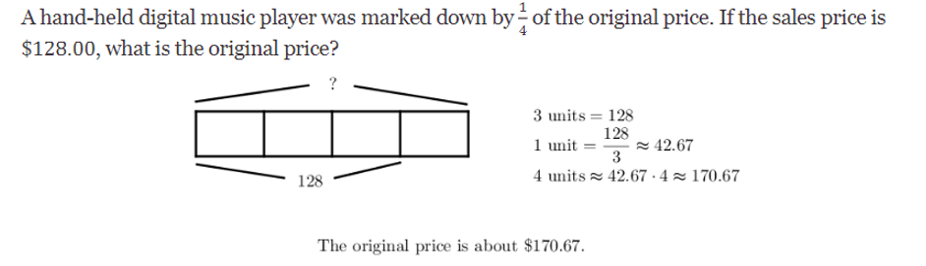
Whenever possible, help students make connections between representations. When they make those connections, students build a deeper and longer lasting understanding about mathematics. Consider the word problem and solution shown. Through questioning and discourse, you can help students make connections from the representation of the problem in words to the tape diagram. How are the numerator and the denominator for the fraction 1/4 represented in the tape diagram? Why is the sale price represented by three sections of the tape diagram? What does the fourth section represent? How does the tape diagram show the original price?

You can also help students make sense of the structure of mathematics, by calling out the connections between models. With guidance, students can see connections such as the relationship between multiplying multi-digit numbers by using an area model and multiplying polynomials by using a tabular model. Ask students to describe the similarities and the differences in the models. Ultimately, students will flexibly use models to solve increasingly complex and abstract problems.

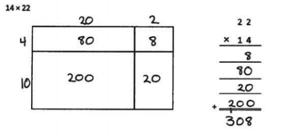
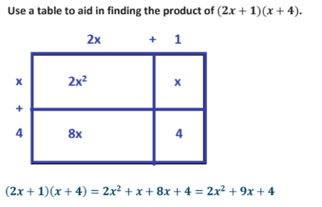
Learn more about Eureka Math models.

Mathematical models can help bridge content across grade levels. For that reason, the Eureka Math curriculum uses models to build a coherent understanding of mathematics. To learn more about the models featured in Eureka Math, see the following webinars and blog posts.

Number Bonds

· Number Bonds: The Foundation of Number Sense (webinar)

· The Number Bond: A K–5 Model That Fosters Number Sense (blog post)

· Kids Need Multiple Strategies to Succeed in Math Class. How the Number Bond Can Be a Powerful Alternative to “Just Adding” (short article)

Tape Diagrams

· Solving Word Problems with Tape Diagrams (webinar)

· Application of the Tape Diagram—A Tool for Problem Solving (blog post)

· To Solve the Problem Below, Try Using a Tape Diagram. It’s an Example of How Different Ways of Doing Math Can Make Hard Problems Easy (short article)

Area Models

· Capitalizing on Prior Knowledge: Using the Area Model to Teach High School Topics (webinar)