Thinking Creatively in Math Class

Finish this sentence: Math class is about . . .

Mathematics instruction can and should emphasize creative problem solving.

The New York Times recently ran an article about a professor at Carnegie Mellon University who stumbled upon an “amazing trick,” known to mathematicians in ancient Babylon, that improves upon the way we all learned to solve quadratic equations in algebra class (Chang & Corum, 2020). It’s a clever approach to factoring binomials that doesn’t require students to memorize and use the quadratic formula.

To me, though, what’s most interesting isn’t the trick itself so much as the way the professor, Po-Shen Loh, went about the process of figuring it out. Loh didn’t begin by analyzing the quadratic formula and looking for shortcuts. Rather, he began by asking himself what quadratic equations represent in the real world. What kind of problem do they allow us to solve, he wondered, and could there be another way to tackle that problem? That is, he gave himself a concrete challenge to overcome: Can I find a new and perhaps easier path to the solution than the formula we’ve all been taught in school?

Compare that to what I heard when I asked a handful of middle school students to finish the sentence, Math class is about . . . “Math class,” said one, is about “getting the right answer.” It’s about “following the steps” and “learning stuff I will never use” and “doing what the teacher says,” others added. “It’s not like classes where we learn stuff we can use for other things,” another explained.

What allowed professor Loh to succeed was something that many of our students don’t even realize they are missing: an appreciation of the creative side of mathematics. As he puts it in a YouTube video that accompanies the Times article, “Mathematics methods and equations can be really beautiful,” especially when they show you new ways of looking at and solving a problem.

But what would it look like to convince students that math can be creative and elegant, rather than just a matter of following “correct” procedures? Think back to your middle school days and picture how you would solve the following equation:

1/3 (x +5) = 5

It’s a safe bet that your path to the solution looks something like this:

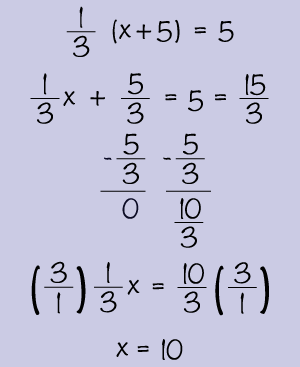
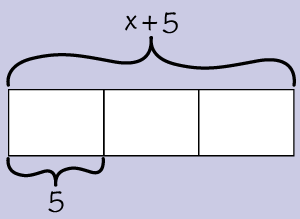
Now, consider the drawing below and ask yourself two questions:

1. Does the drawing accurately represent the equation?
2. Could it offer an elegant new pathway to the solution?

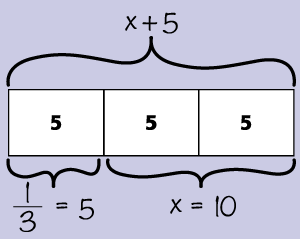
Let me talk you through what I see when I look at this drawing (or “tape diagram”). To begin, I notice that the artist has labeled the whole tape as “x + 5.” I also notice that one-third of that whole (x + 5) has been given the label of “5,” which means the other two-thirds must equal x. And, to answer our first question, that sure looks like an accurate representation of 1/3(x + 5) = 5.

Since I know that thirds are three equal parts of a whole, then I know the other two parts must each have a value of 5, as well. Putting them together, I get 10. That is, x is equal to 10. This process for solving the equation allows me to arrive at the correct answer using simple arithmetic, 5 + 5 + 5 = 15 and 15 – 5 = 10. I don’t need to complete any of the more complex calculations involving fractions as I did with the more traditional algebraic approach.

Understanding how numbers work

Mathematical rules and procedures have been established over time because they consistently represent how numbers work, and each of them represents a past mathematician’s creative, elegant approach to solving a problem that involves relationships among quantities of things in the real world. But if teachers focus solely on abstract formulas and procedures, without conveying the sense of excitement that animated their discovery, then students lose sight of their purpose, and math class become a dreary exercise in “following the steps” and “getting the right answer.”

Students need opportunities to grasp how numbers work beyond the steps in the procedure. They need to see that there are alternative ways to “think through” problems, visualize them, explain the relationship among numbers and symbols, and arrive at solutions. And if we help students gain a deep, conceptual understanding of math, then this can serve them in both expected and unexpected ways.

Tamar Barabi was a 10th grader in Israel when she learned just how exciting it can be to think creatively using mathematics. When presented with a geometry problem, she solved it using what seemed to her to be a simple and logical solution. To her surprise she learned that the proof she created by applying her conceptual understandings and critical thinking, explaining how three radii will always intersect at the center point of a circle, had never been proven before. In fact, her out-of-the-box solution — a new mathematical theorem — was featured in an academic paper published in Pi in the Sky, a journal for the Pacific Institute for Mathematical Sciences, in 2017.

We must not accept the kinds of statements I heard in my conversation with middle school students, who saw math class as nothing more than rule-following. Professor Loh and the Tamar Barabis of the world do not see mathematics as a mindless menu of procedures to be applied. Their discoveries were only possible because they view mathematics as a subject of wonder, curiosity, logic, and exploration. And if we, as educators, were to embrace that sense of purpose and meaning in our own instruction, then our students would be more likely to tell us that “Math class is about thinking creatively about how to use what I know to solve problems.”

References

Barabi, T. (2017). The three radii problem. Pi in the Sky, 20: 26-27.

Chang, K. & Corum, J. (2020, Feb. 6). This professor’s ‘amazing trick makes quadratic equations easier. The New York Times.